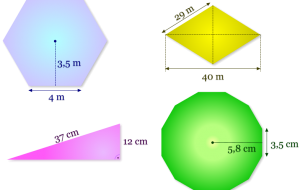
 El área y el perímetro son dos elementos sumamente importantes en las matemáticas. Estos ayudan a cuantificar espacios físicos y ofrecen las bases de matemáticas de mayor avance como la trigonometría, el álgebra y el calculo.
El área y el perímetro son dos elementos sumamente importantes en las matemáticas. Estos ayudan a cuantificar espacios físicos y ofrecen las bases de matemáticas de mayor avance como la trigonometría, el álgebra y el calculo.
El perímetro se define como la medida de la distancia que rodea a una figura, mientras que el área proporciona una idea de la cantidad de superficie que rodea a esa figura.
El conocimiento que ofrece el perímetro y el área es aplicado por muchas personas. Actualmente profesionales como los ingenieros, arquitectos y diseñadores gráficos hacen uso de estos, también puede servir para las personas en general. Tener entendimiento del espacio que se tiene y aprender a utilizar las figuras adecuadamente cuando se compra una casa, se construyen escritorio o se remodela una cocina son una de las aplicaciones de estos elementos.
En palabras simples, el perímetro de una figura que tiene dos dimensiones se define como la distancia que rodea a esa figura. Puede calcularse al sumar cada uno de los lados, siempre que estos posean unidades similares.
El área de una figura que tiene dos dimensiones es calculada contando la cantidad de cuadrados que cubren a ésta. Se han desarrollado diversas fórmulas para saber de forma rápida el área de polígonos estándar, como paralelogramos y triángulos.
Indice
Perímetro de Figuras Geométricas
 El perímetro que tiene una figura de dos dimensiones se define como la distancia que rodea a dicha figura.
El perímetro que tiene una figura de dos dimensiones se define como la distancia que rodea a dicha figura.- Figurativamente sería una cuerda que sigue todos los lados de la figura, la longitud que tiene la cuerda será igual al perímetro.
- Cuando se camina alrededor de un parque, se recorre la distancia del perímetro que tiene el parque.
- Algunas personas relacionan la palabra peri con periferia y metro como medida, eso les ayuda a entender mejor la definición de la palabra y a recordarla de forma más fácil.
- En caso de que la figura sea un polígono, se suman cada una de las longitudes de los lados para obtener el perímetro.
- Todas las longitudes deben tener la misma unidad de medida. El perímetro se mide en unidades lineales, estas representan una única dimensión. Las pulgadas, los pies y los centímetros son ejemplos de unidades de medida de longitud.
Área de Figuras Geométricas
 El área se define como un método que se utiliza para calcular las figuras. Este concepto métrico posibilita otorgar una medida a la extensión de la superficie.
El área se define como un método que se utiliza para calcular las figuras. Este concepto métrico posibilita otorgar una medida a la extensión de la superficie.
Se expresa en unidades matemáticas de medida llamadas unidades de superficie. El área es un término métrico que necesita que el espacio en el cual se especifique o se defina, sea medido. En las superficies planas, este concepto es de mayor intuición.
Toda superficie plana que tenga lados rectos, como un polígono, tiene la posibilidad de ser triangulada y que se calcule su área sumando las áreas de estos triángulos.
De forma ocasional, se utiliza el concepto área como semejanza de superficie cuando no hay confusión entre el término geométrico superficie y la magnitud métrica que se asocia al área.
El área se calcula haciendo uso de fórmulas pertenecientes a cada figura. Son medidas distintas, no se hace uso de cada uno de sus lados, solamente tomando en cuenta la fórmula.
El área de una figura que tiene dos dimensiones define la cantidad de superficie que rodea a la figura. El área se mide en unidades cuadradas con un tamaño fijo.
Loscentímetros cuadrados, las pulgadas y las millas cuadradas son ejemplos de unidades cuadradas. Cuando se tiene el área de un polígono, se cuenta el número de cuadrados de algún tamaño que rodean la región en el interior del polígono.
Perímetros y Áreas de Figuras No Estándar
Para hallar el perímetro de una figura que no es estándar se necesita saber la distancia que rodea a la figura y sumar las longitudes de cada uno de los lados. Para llevar a cabo este procedimiento, la técnica es un poco distinta. Es necesario crear regiones en el interior de la figura en las cuales se pueda hallar el área y luego hacer la sumatoria de cada una de ellas.
Lista de algunas figuras geométricas
- Cilindro
- Circunferencia
- Cono
- Cuadrilátero
- Curva
- Elipse
- Esfera
- Hipérbola
- Parábola
- Pirámides
- Plano
- Poliedro
- Polígono
- Politopo
- Prismas
- Punto
- Recta
- Sección cónica
- Segmento
- Semirrecta
- Sólido de revolución
- Sólidos arquimedianos
- Sólidos platónicos
- Superficie de revolución
- Superficie reglada
- Toro

