 En materia de geometría euclídea, el triángulo rectángulo se define como todo triángulo que tiene un ángulo recto, es decir éste tiene que medir 90 grados. Las razones que existen entre las longitudes de los lados que posee un triángulo rectángulo están enfocadas en la trigonometría plana.
En materia de geometría euclídea, el triángulo rectángulo se define como todo triángulo que tiene un ángulo recto, es decir éste tiene que medir 90 grados. Las razones que existen entre las longitudes de los lados que posee un triángulo rectángulo están enfocadas en la trigonometría plana.
Particularmente, en un triángulo rectángulo se cumple el conocido y popular Teorema de Pitágoras. Se le llama hipotenusa al lado mayor o más grande del triángulo, este es el lado que se opone al ángulo recto.
Los catetos son los dos lados menores del triángulo rectángulo, estos forman parte del ángulo recto. Cada cateto es opuesto a un ángulo agudo. En caso de que la medida de los tres lados de como resultado números enteros, entonces estos forman parte de un trío llamado terna pitagórica.
Indice
Área de un Triángulo Rectángulo
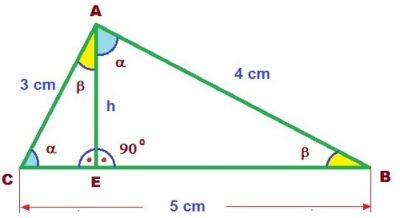
 El área de un triángulo rectángulo se considera como la mitad del área que tiene un rectángulo dividido por su diagonal, como también por un cuadrado cuando el triángulo rectángulo también sea isósceles.
El área de un triángulo rectángulo se considera como la mitad del área que tiene un rectángulo dividido por su diagonal, como también por un cuadrado cuando el triángulo rectángulo también sea isósceles.
La fórmula para encontrar el área de un triángulo rectángulo es: A = b • a / 2
Explicando esta fórmula en detalle: a y b en la ecuación son la representación de las medidas de los dos catetos que tienen coincidencia con los dos lados y con sus alturas correspondientes en el rectángulo.
En cada triángulo rectángulo, sus dos catetos son respectivos con la altura del otro. Tomando en cuenta que a = cateto1 y que b = cateto2, entonces se puede redactar una versión que equivale a la ecuación anterior. Esta es la siguiente: A = cateto1 • cateto2 / 2
La fórmula anterior es sólo para una ocasión especial, se restringe de forma más general para la que se utiliza en cualquier triángulo. Esta es la llamada proposición I.41 de Euclides, ésta se basa en una conceptualización mucho más general de paralelogramo y no está restringido al rectángulo. Esta proposición extiende su validez de la ecuación a cualquier triángulo.
Propiedades de un Triángulo Rectángulo
En cada triángulo rectángulo, se cumplen las siguientes propiedades:
- La hipotenusa es más grande que todos los catetos.
- Poseen dos ángulos agudos.
- La suma del diámetro de un círculo inscrito y de la longitud de la hipotenusa en el triángulo es similar a la suma de la longitud de cada uno de los catetos.
- La longitud que tiene el cuadrado de la hipotenusa es igual a la suma de la longitud que poseen los cuadrados de los catetos.
- La mediana de la hipotenusa desintegra un triángulo rectángulo que es escaleno en dos triángulos: uno acutángulo y otro obtusángulo, no son congruentes pero si son equivalentes.
- En los efectos de área, cualquier cateto puede ser considerado como base mientras el otro cateto se considera como altura.
- Dos triángulos rectángulos que tienen hipotenusa común junto a los ángulos rectos ubicados en semiplanos o puestos definidos por la recta que se compone de la hipotenusa, crean un cuadrilátero birrectángulo.
- La mediana que tiene la hipotenusa que posee un triángulo rectángulo isósceles es descompuesto en dos triángulos rectángulos isósceles equivalentes y congruentes.
- La altura que divide el vértice del ángulo recto tiene coincidencia con un cateto, para tener en consideración al cateto sobrante como una base.
- La mediana que divide el ángulo recto es similar a la mitad que tiene la hipotenusa.
Triángulo Rectángulo en Tres Dimensiones
 Un triángulo rectángulo que se encuentra girando y tiene como generatriz a su hipotenusa y como eje a uno de los catetos, produce un cono de radio similar al cateto que no es axial y una altura semejante al cateto axial.
Un triángulo rectángulo que se encuentra girando y tiene como generatriz a su hipotenusa y como eje a uno de los catetos, produce un cono de radio similar al cateto que no es axial y una altura semejante al cateto axial.
En caso de que dos triángulos rectángulos que se parezcan generen dos conos, en esta situación sus volúmenes serían proporcionales a los cubos de cualquiera de los lados que se correspondan.
De igual forma las áreas se proporcionan a los cuadrados de los lados que les corresponden. Si los dos conos poseen igual eje y un plano secante interseca estos conos y produce dos elipses, estas poseerán ejes proporcionales entre ellos. Lo que quiere decir que son semejantes.

