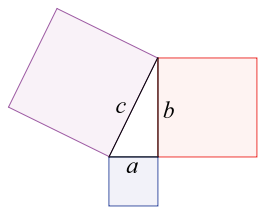
Teorema de Pitágoras: En todo triángulo rectángulo el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos. Pitágoras.El teorema de Pitágoras tiene ese nombre porque su demostración, principalmente, es esfuerzo de la mística escuela pitagórica.
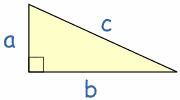
(1)Si un triángulo rectángulo tiene catetos de longitudesy
, y la medida de la hipotenusa es
, se establece que:
De la ecuación (1) se deducen fácilmente 3 corolarios de aplicación práctica:
 |
 |
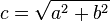 |
El lado más largo del triángulo se llama «hipotenusa», así que la definición formal es:En un triángulo rectángulo (triángulo con un ángulo recto) el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los otros dos lados
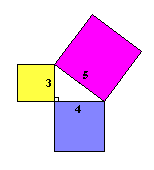
Efectivamente un triángulo de lados de longitudes 3,4,5 tiene un ángulo recto, así que la fórmula se aplica.
Esto se comprueba al observar que las áreas de los cuadrados proyectados a partir de los catetos suman el valor del area proyectada desde la hipotenusa. Ver la figura: 32 + 42 = 52Calculando obtenemos:
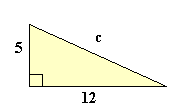
9 + 16 = 25Al conocer las longitudes de dos lados de un triángulo con un ángulo recto, el Teorema de Pitágoras nos permite hallar la longitud del tercer lado. (¡Esto es valido solo en en triángulos rectángulos!)
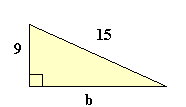
Ejemplos
Llamemos a los lados de los catetos a y b y al lado dela hipotenusa c.(también puede utilizar otras letras x, y, z por ejemplo)
a2 + b2 = c2
Esta formula nos ayuda en álgebra a determinar el valor desconocido de la hipotenusa si es que se conoce el de los dos catetos o el valor desconocido de uno de los catetos si se conoce el de la hipotenusa y el otor cateto. Por ejemplo: