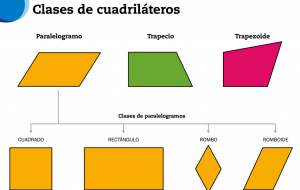
Un cuadrilátero es un polígono que se llega a destacar por las características que presentan sus lados y sus ángulos. Esta figura posee cuatro lados en total, presentando también cuatro ángulos interiores y cuatro ángulos exteriores.
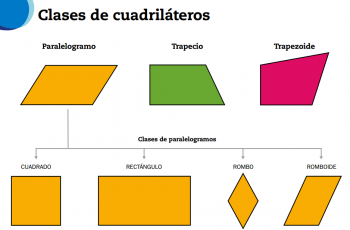
Estos polígonos suelen presentar diferentes formas, sin embargo todas cumplen las mismas características: tienen cuatro vértices, cuatro ángulos interiores, cuatro lados, dos diagonales y la suma de todos sus ángulos da 360 grados. Estas figuras se clasifican en trapecios, paralelogramos, y trapezoides. Los paralelogramos a su vez pueden ser rombo, cuadrado, romboide y rectángulo.
Indice
¿Cuáles son las propiedades de los cuadriláteros?
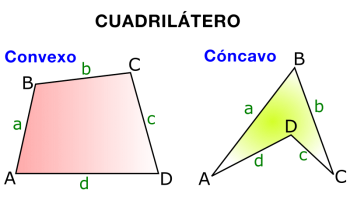Los lados consecutivos son los que tienen en común un vértice.- Los lados opuestos se identifican por ser iguales y porque no poseen un vértice en común.
- Si los cuadriláteros llegan a estar circunscritos, la suma de todos sus lados opuestos son iguales. Ejemplo: AB + CD = BC + DA.
- Los cuadriláteros simples se describen como la unión de dos triángulos que poseen un lado en común, lo cual corresponde a una de las diagonales.
- Los ángulos opuestos y los vértices son aquellos que no forman parte de un mismo lado, por tanto sus ángulos son iguales.
- Cuando las diagonales del cuadrilátero lo seccionan en cuatro triángulos con igual perímetro pasará hacer un rombo.
- Sus diagonales se llegan a cortar en su punto medio.
- Sólo se puede trazar una diagonal desde un vértice.
- La sumatoria de los ángulos interiores llega a ser igual a la suma de sus cuatro rectos, o sea, da como resultado 360 grados.
- A partir de un vértice sólo se podrá trazar una diagonal.
- Los ángulos que son adyacentes a un mismo lado llegan a ser suplementarios, o sea, suman 180 grados.
- Sólo se pueden trazar dos diagonales las cuales se cortan en un punto interior.
Otras propiedades de los cuadriláteros.
Ángulos interiores.
La suma de todos los ángulos internos de un cuadrilátero da en total 360 grados.
Paralelogramos.
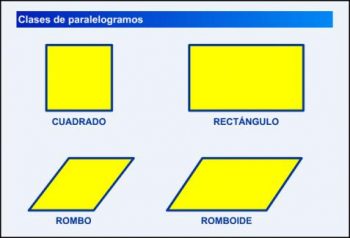Los cuadriláteros son considerados como paralelogramos porque presentan dos pares de lados opuestos paralelos. En esta figura las diagonales se cortan directamente en su punto medio.
El cuadrilátero siempre será un paralelogramo cuando sus ángulos consecutivos son suplementarios, o sea que la sumatoria de sus dos ángulos da 180 grados. La suma de todos los ángulos internos da 180 grados. Así mismo las diagonales en esta figura siempre se bisecan, o sea, se cortan por la mitad.
Trapezoides.
Estas figuras no posee ningún par de vértices opuestos paralelos, razones por lo cual a ciertos cuadriláteros se les considera como un trapezoide.
Trapecios.
Presentan un par de lados opuestos paralelos. Sus lados paralelos se llaman bases. Sus ángulos que llegan a compartir los lados no paralelos llegan a ser suplementarios. Esta base media llega a ser paralela a las bases pero es igual a su semisuma.
En los trapecios isósceles sus diagonales siempre son congruentes, o sea, tienen la misma longitud.
Rectángulo.
Presenta los lados opuestos iguales, sus diagonales son iguales y presenta todos sus ángulos iguales. Las diagonales en esta figura siempre se bisecan y llegan a ser congruentes.
Rombo.
Sus lados son iguales, sus ángulos opuestos son iguales, y los no opuestos son suplementarios. Estos llegan a tener diagonales perpendiculares y presentan bisectrices de los ángulos que llega a interceptar.
La diagonal principal del romboide es bisectriz de los ángulos que intersecta y a la vez es mediatriz de a diagonal secundaria.
Cuadrado.
Presenta todos sus lados y sus ángulos iguales. Sus diagonales son iguales, perpendiculares y se bisecan.
