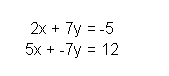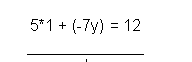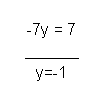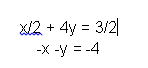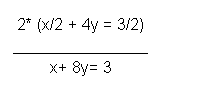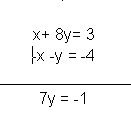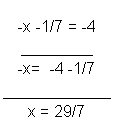El método de eliminación. ¿Qué es? Resolver sistemas de ecuaciones lineales podría parecer difícil para algunos, pero lo cierto es que es muy sencillo si se estudia correctamente. Hoy en día existen muchísimas herramientas que nos ayudan a resolver este tipo de incógnitas, pero nunca serán tan buenas como hacer nosotros mismos las cuentas.
El método de eliminación. ¿Qué es? Resolver sistemas de ecuaciones lineales podría parecer difícil para algunos, pero lo cierto es que es muy sencillo si se estudia correctamente. Hoy en día existen muchísimas herramientas que nos ayudan a resolver este tipo de incógnitas, pero nunca serán tan buenas como hacer nosotros mismos las cuentas.
Existen varios métodos para resolver sistemas de ecuaciones, en este caso vamos a hablar sobre uno que es uno de los más sencillos, de manera que se podrían hacer los cálculos hasta en la mente. Hablamos del método de reducción o mejor conocido como el método de eliminación. Básicamente consiste, como su nombre lo dice, en eliminar alguna de las variables, de manera que se pueda resolver la otra incógnita de la forma tradicional.
Indice
¿Qué es el método de eliminación?
Definición de método de eliminación
Como ya se explicó un poco, consiste en eliminar una de las incógnitas o variables de manera que se pueda resolver la otra de una forma más sencilla.
Si tenemos dos sistemas de ecuaciones lineales con dos incógnitas, es posible sumar ambas ecuaciones de manera que una de ellas se haga 0 por ejemplo, que en una de ellas esté: 2x y en la otra esté un -2x. Al momento de sumarlas nos daremos cuenta de que se anulan ambas, dejándonos sólo una variable.
¿Cómo realizar el método de eliminación?
 Para aplicar el método de eliminación debemos realizar operaciones aritméticas dentro de las ecuaciones para hacer que sean equivalentes. Cuando se hacen equivalentes sabemos que son más fáciles de despejar pues, una de las variables ha desaparecido.
Para aplicar el método de eliminación debemos realizar operaciones aritméticas dentro de las ecuaciones para hacer que sean equivalentes. Cuando se hacen equivalentes sabemos que son más fáciles de despejar pues, una de las variables ha desaparecido.
Para hacer que estas ecuaciones se hagan equivalentes podemos sumar, restar, multiplicar e incluso dividir todos los términos en una ecuación. Es sencillo cuando al menos una de las variables en ambas ecuaciones son equivalentes, entonces sólo debemos sumar ambas.
Por ejemplo:
Si nos fijamos, en este ejemplo podemos eliminar la variable y al sumar ambas ecuaciones. El resultado final sería de esta manera.
Si nos fijamos, en este ejemplo podemos eliminar la variable y al sumar ambas ecuaciones. El resultado final sería de esta manera.
Luego de esto sólo debemos colocar el valor de la variable x, que sabemos que es igual a 1 dentro de cualquiera de las dos primeras ecuaciones y así saber cuál es el valor de y. En este caso utilizaremos la segunda ecuación.
Luego sólo despejamos y nos dará como resultado:
El valor de nuestro sistema de ecuaciones es x=1, y=-1
En el caso de que no sean equivalentes
Si se da el caso de que ambos sistemas no sean equivalentes, hay que convertirlos previamente de manera que se pueda cancelar una variable con otra. Para ello se necesitan realizar las operaciones aritméticas pertinentes. Por ejemplo:
En este caso tenemos dos opciones, se puede dividir la primera ecuación por 2 para luego sumarla a la primera o multiplicar la segunda por 4. La mejor es la primera opción pues se eliminarán los dividendos.
Ahora solo procedemos a hacer la suma que se realizó en el ejemplo anterior, es decir, eliminar la variable x.
Despejamos la variable y y nos quedaría así:
y=-1/7
Ahora que hemos encontrado la variable y, la sustituimos dentro de cualquiera de nuestras ecuaciones, este caso usaremos la segunda.
Acá podemos observar que la variable no es un número entero, por lo que quedaría como x= 29/7. El resultado de este sistema de ecuaciones es y=2, x= 29/7.