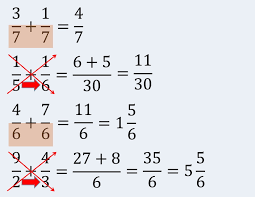La suma es una operación matemática que reúne dos o más números para obtener un total de las cantidades sumadas. A estos números se les llama sumados.
Los números sumados son los valores que se desean combinar. Una fracción es, en matemáticas, el número que expresa una cantidad obtenida de la división de un todo en partes iguales. Es representada por una raya horizontal que separa la primera cantidad (numerador) de la segunda cantidad (denominador).
La suma de fracciones es el proceso de combinar dos o más fracciones en un número equivalente (llamado suma), el cual se representa por el símbolo +. El denominador, en las fracciones, es el número que indica las partes iguales en que la unidad está dividida. Este se escribe debajo del numerador y se separa de este mediante la línea horizontal conocida como también línea divisoria.
Para obtener el valor numérico en forma de fracciones, primero es necesario cambiar todos los denominadores de las fracciones que se van a sumar a su mínimo común denominador (MCD). Después sumamos las fracciones simplemente sumando los numeradores y manteniendo el mismo denominador.
Indice
Suma de fracciones
Ejemplos de suma de fracciones con distinto denominador
1/5 + 2/5 = (1+2)/5 = 3/5
4/8 + 1/8 = 4/8 + 1/8 = (4+1)/8 = 5/8.
Para sumar fracciones con distinto denominador, es necesario saber calcular el mínimo común múltiplo (m.c.m.), que es el número positivo más pequeño que es múltiplo de dos o más números. Los múltiplos de un número son los que se obtienen al multiplicarlo por otros números.
Por ejemplo, los múltiplos de los números 3 y 4..
Para calcular sus múltiplos hay que ir multiplicando el 3 o el 4 por 1, por 2, por 3, etc.
3 x 1 = 3 3x 6= 18
3 x 3 = 9 3 x 7= 21
3×4 = 12 3× 8= 24
3×5 = 15 3× 3 = 27
3× 10= 30
4 x 1 = 4 4× 2 = 8
4 × 3= 12 4 ×4= 16
4× 5= 20 4× 6= 24
4× 7= 28 4× 8= 32
4× 9= 36. 4× 10= 40
Y así sucesivamente hasta infinitos números.
Múltiplos de los números 4 y 5
Para buscar los múltiplos de otros dos números diferentes (como 4 y 5) sería: Los múltiplos de 4 son 4,8,12,16,20,24,28,32,36,40,44, 48, 52, 56, 60, 64, 68, 72, 76, 80, 84, 88, 92, 96, 102,… Mientras que los múltiplos de 5 son 5,10,15,20,25,30,35,40,45,50, 55, 60, 65, 70, 75, 80, 85, 90, 95, 100,…
El número múltiplo más pequeño de 4 y 5 sería el 20.
¿Cómo podemos sumar fracciones con diferente denominador?
Para hacer suma de fracciones con distinto denominador necesitamos seguir por siguientes pasos:
- Primero: Ponemos un denominador común, que será el mínimo común múltiplo de las cantidades.
- Segundo: Multiplicamos cada numerador por el número que hayamos multiplicado al denominador.
- Tercero: Sumamos los numeradores que obtuvimos y dejamos el mismo denominador
Por ejemplo:
Si tenemos las fracciones
4 6
___ + ___
3 5
Lo primero que tenemos que hacer es buscar un denominador común entre 3 y 5, que son los denominadores.Para eso, hallamos el mínimo común múltiplo entre ambos.
Los múltiplos de 3 son: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 41
Los múltiplos de 5 son: 5, 10, 15, 20, 25, 30, 35, 40, m.c.m. (3,5) = 15
El número 15 sería el denominador común de las dos fracciones. Entonces la operación seguirá de la siguiente manera:
4 6
___ + ___ = ___+___
3 5 15 15
Ya que tenemos las fracciones con el mismo denominador, lo siguiente es multiplicar cada numerador por el número que hayamos multiplicado el denominador. Para esto, tenemos que dividir el mínimo común múltiplo entre el denominador inicial y el resultado lo multiplicamos por el numerador de esa fracción;
15 : 3 = 5
4 x 6 = 24
El número 24 es el numerador de la primera fracción.
Para la segunda fracción:
15 : 5 = 3
4 x 6=24
El número 24 es el numerador de la segunda fracción.
4 6 20 18
___ + ___ = ___ + ___
3 5 15 15
Ahora necesitamos hacer la suma de los numeradores:
20+18= 38
Ya que tenemos la cantidad de la sumatoria de los numeradores, el resultado de la suma de estas fracciones con diferente denominador es:
4 6 20 18 38
___+___ = ___+___ = ____.
3 5 15 15 15
