Se llama fracción mixta (y también número mixto) al tipo de expresiones que están compuestas por una parte entera y otra fraccionaria, es decir, es simplemente un número entero y una fracción combinadas en un número «mixto».
Las fracciones se usan en muchas áreas de la vida cotidiana, como por ejemplo en recetas, carpintería, pronósticos del clima, tarjetas de asistencia, y mediciones, por nombrar algunas.
A veces se tienen partes de una unidad que se necesita combinar. De la misma forma en la que se suman números enteros, es posible sumar fracciones y números mixtos. En la suma de fracciones mixtas de igual denominador, el procedimiento más usual es sumar las partes enteras entre sí y las fracciones de igual denominador entre ellas. Por ejemplo: 2 3/4 + 3 2/4 = 5 5/4.
En la suma de fracciones mixtas de diferente denominador, lo primero que hay que hacer es convertir las partes fraccionarias de ambos números mixtos, en fracciones equivalentes (que son aquellas que tienen el mismo valor, aunque parezcan diferentes), con igual denominador. Luego, se procede de la misma manera que al sumar con igual denominador.
Indice
Suma de fracciones mixtas con tres sumandos
Las fracciones comunes son números que se pueden representar como el cociente de dos enteros, donde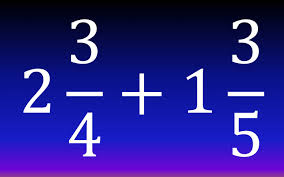 
el numerador representa el dividendo y el denominador, el divisor. Las fracciones impropias pueden tener igual o diferente denominador.
Suma de fracciones con el mismo denominador
Las fracciones mixtas se convierten primero a fracciones impropias. Para realizar una operación de fracciones con el mismo denominador, lo primero que se necesita hacer es multiplicar la parte entera por el denominador, luego se suma el numerador y se deja el mismo denominador.
Después, se suman las fracciones obtenidas, y el resultado puede convertirse en una fracción mixta. Se divide el numerador entre el denominador y se anota el residuo con el mismo denominador.
Suma de fracciones con diferente denominador
Las fracciones mixtas se convierten primero a fracciones impropias. Para sumar fracciones con diferente denominador, se multiplica la parte entera por el denominador, se suma el numerador y se hace la equivalencia para que tengan el mismo denominador, y luego se suman las fracciones obtenidas.
El resultado puede convertirse en una fracción mixta. Se divide el numerador entre el denominador y se anota el residuo con el mismo denominador.
Fracciones mixtas = Fracciones impropias
Es posible usar una fracción impropia o una fracción mixta para escribir la misma cantidad. Por ejemplo 1 3/4 = 7/4.
¿Cómo convertir fracciones de impropias a mixtas y de mixtas a impropias?
En matemáticas las fracciones impropias son mejores que las fracciones mixtas.
Para convertir una fracción impropia en mixta es necesario seguir los siguientes pasos:
- Se divide el numerador entre el denominador.
- Se escribe el cociente como un número entero.
- Se escribes después el resto encima del denominador.
Por ejemplo:
Para convertir la fracción 11/4 en una fracción mixta, se hace lo siguiente:
- Se divide: 11 ÷ 4 = 2 con resto 3
- Se escribe el 2 y después se escribe el resto (3) encima del denominador (4), de la forma siguiente: 2 3/4
Convertir fracciones mixtas en fracciones impropias
Para convertir una fracción de mixta en impropia, es necesario seguir los siguientes pasos:
- Se multiplica la parte entera por el denominador.
- Se suma al numerador.
- Se escribe después el resultado encima del denominador.
Por ejemplo, para convertir la fracción mixta 3 2/5 en fracción impropia
- Se multiplica la parte entera por el denominador: 3 × 5 = 15
- Se suma al numerador: 15 + 2 = 17
- Se escribe después el resultado encima del denominador de la siguiente forma: 17/5
