Los número son aquellos usados para designar una determinada cantidad de elementos que hay en un conjunto. Estos pueden ser número naturales o número negativos. Los número naturales son infinitos, se encuentran a la derecha en la recta numérica y se designan por la letra N, estos son el 0, 1, 2, 3, 4…; y los números negativos son infinitos, están a la izquierda en la recta numérica, y se identifican por su signo de menos, estos son: -1, -2, -3,-4…
Estos número son los usados para contar y ordenar. Sus propiedades se suelen aplicar a la adición y a la multiplicación, las cuales son: la propiedad conmutativa, propiedad asociativa, propiedad de identidad, propiedad distributiva y la propiedad del elemento neutro. Estas propiedades se determinaron cuando se crearon relaciones entre dos números.
Indice
¿Cuáles son las propiedades de los números?
Propiedades conmutativas
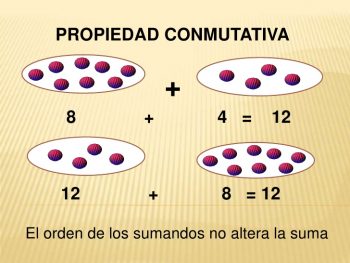El resultado de la suma siempre será la misma sin importar el orden en el cual se suman los números. Por tanto esta propiedad arroja la ley de que el orden de los sumando nunca altera el resultado.
Ejemplo:
4 + 5 = 9, es lo mismo que 5 + 4 = 9.
Del igual forma si se multiplican dos número entre sí, su resultado siempre será el mismo independientemente del orden en que estos números se ubiquen.
Ejemplo:
2 x 4 = 8, es lo mismo que 4 x 2 = 8
Propiedad distributiva
Propiedad que expresa que la suma de dos números agrupados por un tercer número siempre será igual que la multplicación de cada número para luego sumar el resultado.
Ejemplo:
2 x (3 + 5) = 16, es lo mismo que 2 x 3 + 2 x 5 = 16.
Propiedad asociativa
Esta propiedad indica que no importa la forma en que se asocien o se agrupen los números cuando se realiza una suma, puesto a que sus resultados siempre será lo mismo. La ley asociativa específicamente dicta que los números dentro de una expresión aditiva se pueden reagrupar haciendo uso de paréntesis, teniendo en cuenta que cuando se muestran paréntesis estos siempre se deberán de sumar de primero.
Estos paréntesis nunca van a afectar el resultado final, por tanto no importa la cantidad de paréntesis o grupos que se creen nunca se alterará su resultado.
Ejemplo:
6 + (4+3) = 3 + (4 + 6, ambos resultados darán 13.
Esta misma propiedad de los números se aplica en la multiplicación, donde sin importar la forma en que se agrupen los números nunca se llegará a alterar su resultado. En la multiplicación la ley asociativa expresa que todos los números de una expresión de multiplicación se pueden agrupar en paréntesis libremente, ya que esto nunca cambiará su resultado.
Ejemplo:
3 x (2×3) = 2 x (3 x 3), ambas operaciones dará como resultado 18.
Propiedad de identidad
En esta propiedad se llega a expresar que todo número que sea sumado por cero (0) siempre dará el mismo número.
Ejemplo:
124 + 0 = 124.
Esta propiedad también se cumple en la suma, en este caso cualquier número que multiplicado por uno (1) siempre dará el mismo número.
Ejemplo:
124 x 1 =124
Propiedad del elemento neutro
Esta propiedad indica que todo número que sea multiplicado por uno (1) dará como resultado el mismo número.
Ejemplo:
5 x 1 = 5
El elemento neutro para la suma le corresponde al cero (0). Donde sin importar el número que se le suma, sea un entrero negativo o un entero positivo, siempre dará el mismo número.
Ejemplo:
- (-6 ) + 0 = -6
- 0 + (-6) = -6
Elemento opuesto de un número entero
Esta propiedad indica que el elemento opuesto de cualquier número entero siempre será el mismo número pero esta vez marcará el signo opuesto (Op).
Ejemplo:
- En (+1) su opuesto será (-1)
- Op (+8) = (-8)
- (+2) + Op (+2 ) = (+2)+ (-2) = 2 – 2 = 0
A los número enteros opuestos también se les suele llamar como enteros simétricos. En pocos palabras, el opuesto de todo número positivo será uno negativo, mientras que el opuesto de un número entero negativo será uno positivo. Ahora bien el opuesto de cero siempre será cero.
