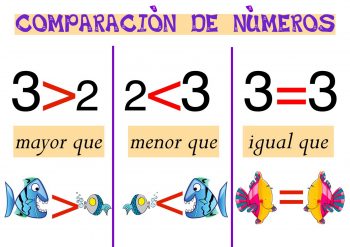
Se conoce como desigualdad a aquella expresión matemática que posee un signo de desigualdad, teniendo en cuenta que los signos de desigualdad son ≠ (no es igual?; ≤ (menor o igual que), ≥ (mayor o igual que), < (menor que) , > (mayor que).
Esta se utiliza para representar que una cantidad es mayor o menor que otra cantidad.
Indice
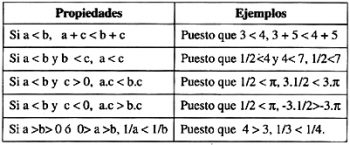
Propiedades de las desigualdades
Propiedad aditiva de las desigualdades
La desigualdad nunca varía al restar o sumar la misma cantidad de ambos lados.
Esta propiedad indica que al sumar o restar los dos miembros de una desigualdad por un mismo número, su resultado siempre será otra desigualdad del mismo sentido.
Propiedad multiplicativa de las desigualdades
- La desigualdad puede variar su sentido cuando se divide o se multiplica por un número negativo
Propiedad que establece que al dividir o multiplicar dos miembros de una desigualdad con un número negativo el resultado que se obtendrá cambiará de sentido.
El sentido en este caso solo se conserva cuando se divide o se multiplica ambos miembros de la desigualdad con un número positivo, ahora bien si se realiza la operación con un número negativo se invertirá el proceso.
- No hay variación en la desigualdad en cuanto a su sentido si se divide o se multiplica por un número positivo
En esta propiedad se expresa que al dividir o al multiplicar dos miembros de una desigualdad por un número positivo se tendrá como resultado una desigualdad equivalente a la primera.
Propiedad del inverso de las desigualdades
Si ambos miembros de una desigualdad son positivos o negativos se crea un inverso multiplicativo, obteniéndose así otra desigualdad con un sentido diferente que la primera.
Ahora bien, si ambos miembros de la desigualdad son positivos y se elevan con un exponente par y positivo, su resultado será otra desigualdad pero siempre tendrá el mismo sentido de la primera.
Propiedad de extracción de raíz cuadrada
Propiedad que indica que al tener los dos miembros de una desigualdad signos contrarios y que se encuentran elevados a un exponente par el sentido de la igualdad resultante será indeterminado.
Todo número positivo será mayor que 0
Esta propiedad indica que todo número que dentro de la recta númerica se encuentra a la derecha del cero, siempre será mayor que cero. Esta se representa con el símbolo de desigualdad >.
Ejemplo:
- 5 > 0.
- 25 > 0.
Todo número negativo es menor que cero
Indica que todo número que se encuentra a la izquierda del cero en la recta numérica siempre será menor que O. Ejemplo:
- -9 < 0.
- -5 < 0.
Entre dos número negativos el que tiene menor valor absoluto será el mayor.
Esta propiedad indica que todo número negativo que se encuentre próximo al cero siempre será el mayor.
Ejemplo:
- -5 > -10.
- -8 > -30.