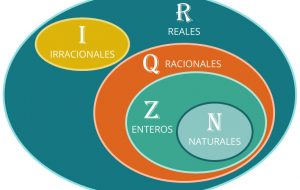
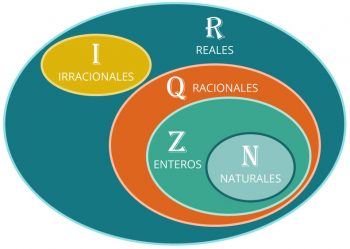
 Un números real, denotado por el símbolo R, es el conjunto conformado por los números racionales e irracionales. El conjunto de los números reales pertenece en matemáticas a la recta numérica que comprende a los números racionales y a los números irracionales.
Un números real, denotado por el símbolo R, es el conjunto conformado por los números racionales e irracionales. El conjunto de los números reales pertenece en matemáticas a la recta numérica que comprende a los números racionales y a los números irracionales.
Esto quiere decir que incluyen a todos los números positivos y negativos, el símbolo cero, y a los números que no pueden ser expresados mediante fracciones de dos enteros que tengan como denominador a números no nulos (excluye al denominador cero).
Indice
¿Cuáles son las propiedades de los números reales?
Propiedad de la sustracción
Al realizar una resta o sustracción con números reales siempre se toma en cuenta sus propiedades que llegan a ser reglas de gran importancia para que el resultado siempre sea el correcto, estas son:
 En la resta de dos números positivos, si el minuendo es menor su resultado será un número natural negativo.
En la resta de dos números positivos, si el minuendo es menor su resultado será un número natural negativo.- Si el minuendo es mayor al restar dos números enteros positivos, su resultado será otro número positivo.
- Si se resta un número negativo con uno positivo, siendo el minuendo el negativo, su resultado deberá ser un número entero negativo.
Propiedad de la adición
En toda suma de números racionales siempre se hacen presentes sus propiedades, estas son:
- Propiedad conmutativa: esta llega a indicar que el orden en el cual se ubiquen los sumando nunca llegará a alterar el producto. Ejemplo: a + b + c = c + b + a.
- Propiedad interna: esta indica que el resultado de la suma entre dos número reales siempre dará un número real.
- Propiedad asociativa: es la que expresa que no importa la sociedad creada entre los sumando para hacer la operación, ya que sin importar la asociación que se sume primero siempre dará el mismo resultado, el cual además será un número real. Ejemplo: a + (b+c) = c +(a +b).
- Propiedad del elemento inverso o neutro: indica que todo número real llega a tener un inverso u opuesto aditivo, donde al sumar el número con su inverso su resultado será 0.
Propiedad neutral: Indica la existencia del elemento neutro en la suma, donde se expresa que el elemento neutro de toda suma es el cero, ya que todo numero que es sumado a este siempre dará el mismo número. Ejemplo: 1 + 0 = 0.
Propiedades de la división
 La división no cumple con la propiedad conmutativa ni con la asociativa, ya que su resultado cambia.
La división no cumple con la propiedad conmutativa ni con la asociativa, ya que su resultado cambia.- La división de un número natural con el cero no existe.
- Al dividir el cero con un número natural da cero.
- Presenta las mismas reglas de los signos que la multiplicación.
Propiedades de la multiplicación
Al multiplicar se reconocen las propiedades siguientes:
- Propiedad conmutativa: no importa el orden en que dos números reales se multipliquen su resultado siempre es el mismo.
- Propiedad interna: indica que la multiplicación de dos números reales siempre será otro número real.
- Propiedad asociativa: expresa que no importa la forma en que se agrupen los números para realizar la multiplicación, su resultado siempre será el mismo.
- Propiedad del elemento neutro: la multiplicación de un número real con el 0 o con el 1, siempre dará el mismo número real.

