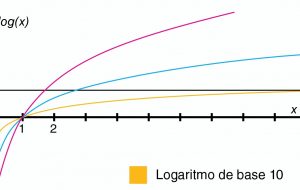
 El logaritmo es el exponente que se muestra en una potencia con cierta base. Se trata del número que indica las veces en la cual la base debe ser elevada para así obtener un determinado número. Se trata de una función inversa a la función exponencial.
El logaritmo es el exponente que se muestra en una potencia con cierta base. Se trata del número que indica las veces en la cual la base debe ser elevada para así obtener un determinado número. Se trata de una función inversa a la función exponencial.
En los cálculos, resulta que el logaritmo de un producto es igual a sumar los logaritmos de sus factores; el de un cociente es igual a restar al logaritmo del dividendo el del divisor. El de una potencia es igual al producto del exponente multiplicado por el logaritmo de la base. El logaritmo de la raíz enésima de un número x determinado, resulta de dividir el logaritmo de x por el índice m de la raíz.
Indice
- 1 ¿Cuáles son las propiedades de los logaritmos?
- 1.1 Siempre se presentan como logaritmos positivos
- 1.2 Dos números diferentes siempre tendrán diferentes logaritmos
- 1.3 Se escriben con números reales positivos
- 1.4 Logaritmo de la base
- 1.5 Logaritmo de un producto
- 1.6 Logaritmo de la unidad
- 1.7 Logaritmo de potencia de igual base
- 1.8 Logaritmo de una raíz
- 1.9 Logaritmo de un cociente
- 1.10 Logaritmo de una potencia
¿Cuáles son las propiedades de los logaritmos?
Siempre se presentan como logaritmos positivos
Toda base siempre presenta logaritmos positivos, ya que no existen logaritmos con números negativos.
 Dos números diferentes siempre tendrán diferentes logaritmos
Dos números diferentes siempre tendrán diferentes logaritmos
Si P es diferente que Q sus logaritmos serán diferentes, o sea que el loga P no será igual que loga Q.
Se escriben con números reales positivos
Tanto la base como el argumento de un determinado logaritmo siempre se presenta como números reales positivos. La base nunca puede ser 1.
Logaritmo de la base
El logaritmo correspondiente a la base será igual a 1.
Logb(b)=1
Logaritmo de un producto
El logaritmo de un determinado producto siempre será lo mismo que la suma de los logaritmos de los factores.
Logb(a.c)=lobba + logb c.
Logaritmo de la unidad
 Siempre el logaritmo de 1 será igual a cero sin importar su base.
Siempre el logaritmo de 1 será igual a cero sin importar su base.
Logb(1)=0
Logaritmo de potencia de igual base
El logaritmo de una potencia de un determinado número llegará a ser el mismo que el producto entre el logaritmo del número y el exponente de la potencia.
Logbbn= n
Logaritmo de una raíz
El logaritmo de una raíz siempre será el mismo que la división de la cantidad subradical entre el índice de la raíz.
Logaritmo de un cociente
 El logaritmo que le corresponde a un cociente siempre será lo mismo que la diferencia entre el logaritmo del dividendo y el logaritmo del divisor.
El logaritmo que le corresponde a un cociente siempre será lo mismo que la diferencia entre el logaritmo del dividendo y el logaritmo del divisor.
Logb(p/q) = logbp – logbq
Logaritmo de una potencia
El logaritmo de una potencia siempre será el mismo que el resultado de la multiplicación del exponente con el logaritmo de la base.
Logacn =n logac

