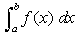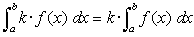 Una integral definida es lo que se hace cuando se calcula el valor de las áreas que están limitadas por rectas y curvas. La integración se presenta como el proceso invertido de la diferenciación, la cual da cierta libertad para dirigir en el espacio.
Una integral definida es lo que se hace cuando se calcula el valor de las áreas que están limitadas por rectas y curvas. La integración se presenta como el proceso invertido de la diferenciación, la cual da cierta libertad para dirigir en el espacio.
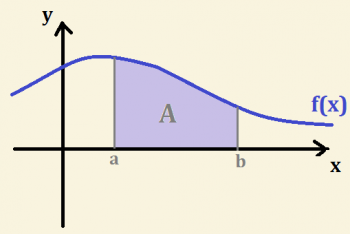
Las integrales definidas se distinguen porque presentan un parámetro definido o ciertos puntos de integración definidas con la cual se encuentra el valor del área bajo f (x), que corresponde a la curva de una función.
La integral se representa a través de la fórmula:
Donde:
∫ corresponde al signo de integración.
- a es el límite inferior.
- b es el límite superior de la integración
- dx llega a ser el diferencial de x, este llega a mostrar la variable de esa función que se está integrando.
- f(x) llega a ser la función a integrar o el integrando.
¿Cuáles son la propiedades de la integral definida?
 Existen varias propiedades con las cuales se puede determinar o dar solución al área que se encuentra definida por la función sea de una curva, de una recta, etc., donde según los datos que llega a mostrar el problema se logra solucionar la integral definida usando una determinada integral acorde al caso que se esté enfrentando.
Existen varias propiedades con las cuales se puede determinar o dar solución al área que se encuentra definida por la función sea de una curva, de una recta, etc., donde según los datos que llega a mostrar el problema se logra solucionar la integral definida usando una determinada integral acorde al caso que se esté enfrentando.
Siempre se ha de tener en cuenta que la integral siempre será positiva cuando la función es mayor que cero, si dicha función es menor la integral pasará a ser negativa.
Entre estas propiedades se destacan:
Cualquier integral que es extendida hacia un intervalo a partir de un solo punto siempre será igual a cero.
La integral que resulta con la suma de funciones siempre será igual a la suma de cada integral seleccionado por separado, o sea, que la integral definida en una suma de funciones siempre será la misma que la suma de integrales.
Cuándo se permuta cada uno de los límites de una integral, la misma cambiará de signo.
Al multiplicar una constante por una función la integral que se obtiene como producto será igual a la constantes por la integral de a función.
Si C llega a ser un punto interno del intervalo [a, b], la integral definida en este caso se descompondrá como una suma de dos integrales que serán extendidas a los intervalos [a, c] y [c, b].