 Los exponentes, también llamados índices o potencias, es aquel número que se suele ir a la derecha y encima de otro número al cual se nombra como base, indicando la cantidad de veces que esta base deberá de ser multiplicada por sí misma. Ejemplo: 62 indica que la base 6 deberá ser multiplicada dos veces, 6 x 6, lo cual dará como resultado 36.
Los exponentes, también llamados índices o potencias, es aquel número que se suele ir a la derecha y encima de otro número al cual se nombra como base, indicando la cantidad de veces que esta base deberá de ser multiplicada por sí misma. Ejemplo: 62 indica que la base 6 deberá ser multiplicada dos veces, 6 x 6, lo cual dará como resultado 36.
62 se lee en palabras 6 a la segunda potencia, 6 a la potencia 2, o puede leerse de la siguiente forma: 6 al cuadrado.
La ley de los exponentes expresa que:
- El exponente indica la cantidad de veces que la base debe ser multiplicada por sí misma.
- El exponente fraccionario como es el caso del 1/n significa hacer la raíz n-ésima: y1/n= n raíz de x.
- Como lo contrario de multiplicar es dividir, cuando se muestra un exponente negativo indica que hay que dividir.
Indice
¿Cuáles son las propiedades de los exponentes?
Producto de potencias
 Se refiere a la propiedad que indica que al multiplicar dos potencias que presentan igual base, siempre se ha de sumar sus exponentes.
Se refiere a la propiedad que indica que al multiplicar dos potencias que presentan igual base, siempre se ha de sumar sus exponentes.
Ejemplo:
- Ya . Yb = Ya+b
- 102 . 105 = 102+5 = 107
Potencia de un cociente
Es la propiedad que llega a indicar que al calcular la potencia de un cociente, solo se ha de dividir las potencias del numerador con el del denominador.
Ejemplo:
- (x/y)a= xa/yb
- (6/3)2= 62/ 32.
Propiedades de la potencia de una potencia
Es la propiedad que llega a expresar que para hallar la potencia de una potencia se debe de multiplicar los exponentes.
Ejemplo:
- (Ya)b = Ya.b
- (254)2= 254.2 = 258
Cociente de potencias
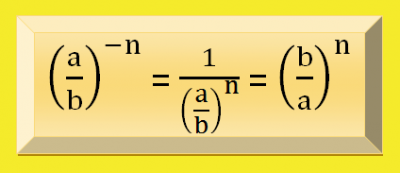 En esta propiedad de los exponentes se llega a especificar que al dividir dos potencias que tengan igual base, solo se ha de restar sus exponentes.
En esta propiedad de los exponentes se llega a especificar que al dividir dos potencias que tengan igual base, solo se ha de restar sus exponentes.
Ejemplo:
- Ya/Yb = Ya-b
- 24/ 22 = 24-2 = 22.
Exponentes cero
Esta propiedad indica que toda base elevada a la potencia de cero es uno.
Ejemplo:
60 x 61 = 6(0+1)= 61
En pocas palabras todo valor que sea elevado a la potencia de cero es uno, siempre y cuando la base sea distinta de cero.
Por otro lado, todo valor que sea elevado a la potencia de uno siempre será el mismo valor. Ejemplo: a1 = a , (-a)1=-a
Potencia de un producto
 Es la propiedad que llega a indicar que al calcular la potencia de un producto solo hay que multiplicar las potencias de sus factores.
Es la propiedad que llega a indicar que al calcular la potencia de un producto solo hay que multiplicar las potencias de sus factores.
Ejemplo:
- (X . Y)a= Xa.Yb
- (4 x 2)4= 44 x 24
Para conocer el resultado de 44 x 24 solo hay que simplificar cada dígito de la siguiente forma.
(4 x 4 x 4 x 4) x (2 x 2 x 2 x 2) = 44 x 24

