 Una parábola se define como la línea curva en la que sus puntos se encuentran equidistantes a un foco localizado en la parte interior de la curva, y a una recta conocida como directriz que se localiza en el lado perpendicular y exterior a la parábola.
Una parábola se define como la línea curva en la que sus puntos se encuentran equidistantes a un foco localizado en la parte interior de la curva, y a una recta conocida como directriz que se localiza en el lado perpendicular y exterior a la parábola.
De manera geométrica, forma parte de una sección cónica que tiene excentricidad igual a 1. Los tres elementos principales que forman parte de una parábola son la directriz, el foco y el eje.
Otros elementos que componen a la parábola son el vértice, parámetro, cuerda, distancia focal, lado recto, cuerda focal y sus puntos.
Gracias a estos elementos es posible calcular propiedades y longitudes que tienen las parábolas. Cada una de las parábolas son similares en su nivel geométrico debido a que cada una corresponde a una sección cónica que tiene la misma excentricidad. La única diferencia que se distingue entre una y otra es la escala con la cual se trabaje.
Usualmente durante el estudio de la física, las matemáticas y la geometría, las parábolas se dibujan a mano, sin prestar atención a algunos parámetros. A causa de esto, la mayoría de las parábolas aparentan tener un ángulo o una forma distinta. Esta forma geométrica normalmente se considera una elipse, en la que uno de sus vértices se encuentra en el infinito, de igual forma que en el centro de la curva.
Indice
Elementos que forman parte de una parábola
Eje
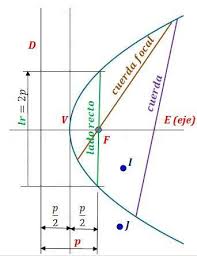 Se define como el eje simétrico de la parábola. El punto donde el eje divide a la parábola se conoce como vértice.
Se define como el eje simétrico de la parábola. El punto donde el eje divide a la parábola se conoce como vértice.
Foco
Es el punto localizado en el eje. Cualquier punto de la parábola se encuentra a la misma distancia de la directriz y del foco.
Parámetro
Es la línea paralela al eje y perpendicular a la directriz que crea un vector entre la directriz y el foco.
Directriz
Es la línea que se encuentra perpendicular al eje y está opuesta a la parábola. En caso de que se ubique en algún punto de la parábola para trazar una línea hasta llegar al foco, la longitud de la misma será similar a una línea trazada hasta llegar a la directriz.
Distancia focal
Es la distancia que existe entre el vértice y el foco, es equivalente al valor del parámetro cuando se divide entre 2.
Vértice
Este es el punto de intersección en el cual se cruzan la parábola y el eje. El vértice de una parábola se ubica en el punto medio entre la directriz y el foco.
Cuerda focal
Es la cuerda que conecta 2 puntos de una parábola atravesando el foco.
Cuerda
Es cualquier línea recta que conecte 2 puntos en la parábola.
Puntos
Cuando se traza una parábola, se crean dos espacios visualmente diferenciables que se encuentran a ambos lados de la curva. Estos dos lados forman los puntos exteriores e interiores de la parábola. Los cuales se definen como:
- Puntos exteriores: se localizan en la parte externa entre la directriz y la parábola. Es un punto singular que no forma parte de la parábola en si. Es considerado un punto fijo de referencia que se ubica encima del eje focal.
- Puntos interiores: se ubican en el lado de la parte interna de la curva.
Trazado de una parábola
Los puntos equidistan del foco y de la directriz, por lo tanto se realizan trazas paralelas a la directriz a cualquier distancia y los arcos con centro en el radio y en el foco de la distancia hasta que se corten las rectas. Estos puntos formarán parte de la parábola por equidistar a la directriz y al foco. Cuando se dibujen, se conectan entre sí a mano alzada o a través de plantillas de curvas.

