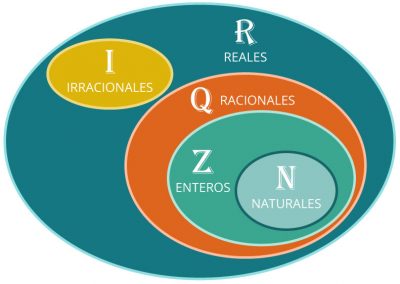
La clasificación de los números reales está dividida en los números enteros, números naturales, números irracionales y los números reales. Los números reales se representan con la letra R.
Los números reales son la combinación que tienen los grupos de números irracionales y racionales. Para crear estos grupos, es necesaria la intervención de números enteros y números naturales.
Existen diversas maneras en las que diferentes números reales pueden ser descritos o construido, van desde una forma sencilla hasta otra más compleja, tomando en cuenta el trabajo matemático que se desee llevar a cabo.
Indice
Clasificación de Números Reales
Números naturales
Los números naturales se usan para contar.
- Por ejemplo: hay 7 pelotas en el estadio.
Existen definiciones de números naturales que empiezan su conteo en el 0, mientras que otras empiezan con el 1.
Los números naturales son los que se emplean para contar, se utilizan como números cardinales o números ordinales desde el 1, 2, 3, 4, 5, 6, 7… hasta el infinito.
Los números naturales sirven de base en la que otros conjuntos de números se construyen por extensión, tales como los números racionales, los números enteros, los números enteros, los números reales y muchos más. Estas cadenas de extensiones son las que conforman a los números naturales de forma canónica y se identifican en los demás sistemas de números.
Números enteros
Los números enteros son las cantidades que se escriben sin utilizar un componente fraccional. Por ejemplo: 7, 9, 22, 0, -13, etcétera. Por otro lado las cantidades como √2 y 9.5 no se consideran números enteros.
Se entiende que los números enteros abarcan a los números completos, incluyendo a los negativos que tienen los números naturales. Se usan para expresar profundidades relacionadas a la temperatura bajo cero o al nivel del mar, a dinero por pagar, entre otras cosas.
Un conjunto de números enteros incluye al 0, a los enteros negativos y a los números naturales positivos. Normalmente esto se representa con una letra Z, normal o en negrita. Los números enteros componen el grupo de menor tamaño y el conjunto más pequeño que tienen los números naturales. Según la teoría de los números algebraicos, los números enteros en ocasiones se llaman enteros irracionales para establecer diferencias de los enteros algebraicos.
Números racionales
Un número racional es cualquier cantidad que se expresa como fracción o componente de dos números que son enteros (p/q).
El numerador p y el denominador q. Debido a que q puede ser igual a 1, entonces cada número entero también es un número racional. El conjunto de números racionales, también llamado “los racionales” se representan con una Q.
La expansión decimal que tiene un número racional termina siempre luego de un número finito de cantidades o cuando se empieza a repetir igual secuencia finita de dígitos constantemente. Adicional a esto, cualquier terminal o decimal que se repita es una representación de una cantidad racional.
Los números racionales, junto a la multiplicación y la suma crean campos que conforman a los números enteros y se contienen por cualquier rama que los incluya.
Números irracionales
Se define como número irracional a todos los números reales que no son racionales. Este tipo de números no puede expresarse como fracción. Los números racionales son números que se componen de fracciones con números enteros.
La prueba de Cantor expresa que cada número real es no numerable y que los racionales si lo son, entonces se entiende que prácticamente todos los números reales también son irracionales.
En los números irracionales se encuentran el número de Euler (e), el radio π de una circunferencia y de su diámetro y círculo, la raíz cuadrada de 2 y el número áureo (φ). Cada una de las raíces cuadradas que tienen los números naturales también son irracionales. Sólo existe una excepción y son los cuadrados perfectos.
Es posible observar que los números irracionales que se expresan de forma posicional dentro de un sistema numeral, como los números decimales, no se repiten ni terminan. Esto significa que no se componen de una secuencia de dígitos, por esto la repetición crea una línea representativa.
