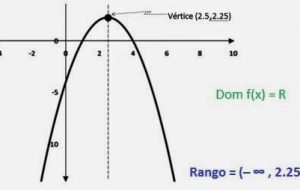
 El dominio de una función se representa por f (x), se define como el conjunto de cada uno de los valores que definen a la función el recorrido o el rango de la función se conoce como el conjunto de los valores reales que tiene la variable y, también reconocida como f (x).
El dominio de una función se representa por f (x), se define como el conjunto de cada uno de los valores que definen a la función el recorrido o el rango de la función se conoce como el conjunto de los valores reales que tiene la variable y, también reconocida como f (x).
Cada una de estas funciones está compuesta por dos clases de variables, las cuales son: variables dependientes y variables independientes. Estos valores dependen básicamente de las variables independientes.
Los valores válidos que existen para una variable independiente x se conocen por el nombre de el dominio. Los valores válidos que tiene una variable dada independiente y son llamados el rango. El rango y el dominio de una función comúnmente se encuentran limitados por la naturaleza que tenga la relación.
El dominio de una relación o función es el conjunto de cada uno de los valores independientes posibles que puede tener una relación, todas las entradas que pueda. El rango de una relación o de una función es el conjunto de cada uno de los valores dependientes posibles que pueda producir una relación, cada una de las salidas posibles. Cuando se colocan las salidas y las entradas en grupos divididos, el rango y el dominio posibilitan la exploración de patrones de cada una de las clases de variables.
Indice
Explicación del Dominio y del Rango
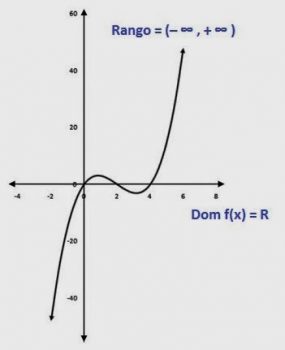 Las funciones y las relaciones explican la interacción que ocurre entre las variables ligadas. Estas relaciones agrupan las entradas y los valores independientes, estas son las variables que pueden controlarse a través de las circunstancias.
Las funciones y las relaciones explican la interacción que ocurre entre las variables ligadas. Estas relaciones agrupan las entradas y los valores independientes, estas son las variables que pueden controlarse a través de las circunstancias.
También, se encuentran las salidas y los valores dependientes que son las variables definidas por los valores independientes.
Hay otros pares de componentes que se deben tomar en cuenta cuando se habla de relaciones, estos son el rango y el dominio. Cuando se colocan las salidas y las entradas en grupos alejados unos de los otros, el rango y el dominio posibilitan poder explorar patrones que se encuentran en cada una de las variables distintas.
Dominio y Rango representados en Conjuntos y Tablas de Pares Ordenados
Las relaciones pueden ser explicadas a través de conjuntos o tablas de pares ordenados. Hallar el rango y el dominio en estos casos es muy fácil, siempre que se tenga en cuenta lo que significan cada uno de los términos. En caso de que en una relación matemática se utilice una tabla, los valores independientes normalmente se ubican en la parte de la columna de la izquierda, mientras que los valores dependientes suelen colocarse en la columna de la derecha.
Cuando son conjuntos de pares ordenados, solamente se necesita dividir los pares en coordenadas (y) y coordenadas (x). Las coordenadas x representan los valores independientes que proporcionan el dominio. Las coordenadas y son la representación de los valores dependientes que son iguales al rango.
Dominio y Rango representados en Gráficas
Las relaciones y las funciones también pueden ser representados con gráficas. La cantidad independiente usualmente se grafica ubicándose en el eje horizontal x, lo que quiere decir que los puntos en esta coordenada son del dominio. Mientras que la cantidad dependiente usualmente se grafica ubicándose en el eje vertical y, estas coordenadas definen el rango.
Sumario
Las funciones pueden explicarse haciendo uso de símbolos, palabras, conjuntos, gráficas o tablas de pares ordenados; pero en cada uno de estos casos las características son iguales. El dominio es el valor independiente o la entrada, es lo que inicia a la función. El rango es el valor dependiente o la salida, es lo que se obtiene de la función. El rango y el dominio se pueden encontrar limitados con pocos valores discretos o pueden tener cada uno de los números reales hasta llegar al infinito.

