 Ángulo consiste en un concepto matemático que es parte de una de sus disciplinas, concretamente, la geometría. Consiste en la fusión de dos líneas cuyo origen es compartido.
Ángulo consiste en un concepto matemático que es parte de una de sus disciplinas, concretamente, la geometría. Consiste en la fusión de dos líneas cuyo origen es compartido.
De esta forma, un ángulo está integrado por los dos lados que lo forman y por su vértice, o sea, el punto que los une. Para su denominación se suelen usar las letras en mayúsculas.
Es importante destacar que no todos los ángulos son similares ni miden igual. Es probable su medición en radianes o grados. Para calcularlos en grados se requiere el uso de un transportador (instrumento en forma de semicírculo graduado de 180 grados). Todas las medidas que se tomen con dicha herramienta son propias del sistema sexagesimal.
Indice
Ángulos opuestos por el vértice
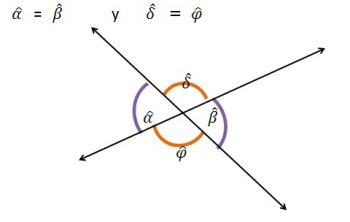 Se conocen como ángulos opuestos por el vértice cuando los lados de uno son semirectas, opuesto a los lados del otro. Los ángulos opuestos al vértice tienen como característica que todos los ángulos opuestos por el vértice son similares.
Se conocen como ángulos opuestos por el vértice cuando los lados de uno son semirectas, opuesto a los lados del otro. Los ángulos opuestos al vértice tienen como característica que todos los ángulos opuestos por el vértice son similares.
Esta cualidad es una de las más simples en el área de la geometría, se puede usar cuando dos rectas se cruzan. En caso de que un par de rectas se crucen, van a crear cuatro ángulos menores a 180 grados.
Estos ángulos van a tener un espacio en común el cual se conoce como vértice, en este punto es donde se cortan dos rectas. Si dichas rectas son perpendiculares entre sí, los cuatro ángulos serán rectos, en caso de que las rectas no sean de esta forma, entonces dos de los ángulos serán obtusos y dos agudos.
Cada ángulo agudo debe tener en común el vértice y un lado con cada uno de los ángulos obtusos; de igual forma, un ángulo de tipo obtuso tendrá en común el vértice y un lado con cada ángulo agudo; de igual manera, un ángulo agudo y uno obtuso deben sumar 180 grados, ya que tienen un lado en común y los otros lados son parte de la misma recta.
Otros tipos de ángulos
Ángulos adyacentes
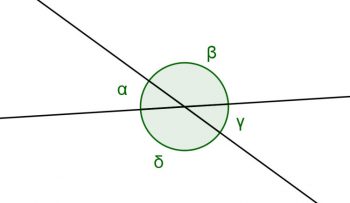 Consisten en ángulos consecutivos que al sumarse dan como resultado 180 grados. O sea, comparten el vértice y un lado, y los otros lados son casi rectas opuestas. Es muy común utilizar los conceptos ángulos adyacentes, contiguos y consecutivos como sinónimos en la práctica.
Consisten en ángulos consecutivos que al sumarse dan como resultado 180 grados. O sea, comparten el vértice y un lado, y los otros lados son casi rectas opuestas. Es muy común utilizar los conceptos ángulos adyacentes, contiguos y consecutivos como sinónimos en la práctica.
Ángulos opuestos
De igual forma conocido como ángulos verticalmente opuestos o ángulos verticales. Los ángulos opuestos se presentan cuando dos líneas se cruzan creando una X o algo parecido. Al cruzarse dos líneas, se manifiestan cuatro ángulos.
En esta situación, los ángulos opuestos poseen la misma medida, o sea, se consideran ángulos congruentes, y los ángulos adyacentes son complementarios, puesto que, al sumarlos, siempre da 180 grados.
Ángulos convexos y cóncavos
Los ángulos que van desde 0 hasta 180 grados se conocen como saliente o convexo, en tanto que los ángulos superiores a 180 grados, pero menores de 360, son entrantes o cóncavos. A los ángulos cóncavos también se les conoce como ángulos reflejos.
¿Cómo mediar ángulos?
 Poner el transportador en el área superior del vértice de un triángulo con la marca central de la zona interna (que es el área recta) en el vértice. Un vértice consiste en el punto en el que dos de los tres lados de un triángulo se dividen.
Poner el transportador en el área superior del vértice de un triángulo con la marca central de la zona interna (que es el área recta) en el vértice. Un vértice consiste en el punto en el que dos de los tres lados de un triángulo se dividen.
Rotar el transportador, conservando la marca del centro en el vértice para alinear una de las dos líneas del ángulo con la de la base en el instrumento.
Mirar el ángulo para establecer si es menor o mayor de 90 grados. Este ángulo, o recto, posee una figura de L. Si el ángulo es mayor de 90 se conoce como ángulo obtuso; en tanto que un ángulo agudo es menor de 90 grados.
Ver la medición en el área superior curvado del transportador donde el ángulo se enfila en la escala. Usar el conglomerado superior de números para los ángulos mayores de 90 grados y los números menores para los ángulos inferiores a 90.

